TEOREMA BAYES

Seandainya ruang sampel, S, dipartisi menjadi k, yaitu 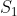 ,,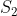 , ... , ( 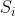dan  saling asing) dan A adalah suatu peristiwa di dalam S, maka A bisa dinyatakan sebagai berikut :

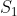                      A = (A ∩ 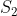) ∪ (A ∩ ) ∪ (A ∩ ) ∪ ... ∪ (A ∩ )

Sehingga :

                        P(A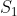) = P (A ∩ 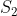) + P (A ∩ ) + P (A ∩ ) + ... + P(A ∩ )

                        P(A) = P(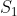) P(A| 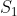) + P(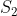) P(A|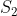) + ... + P( )P(A| )

Sebagai ilustrasi :
A dan B adalah 2 kejadian yang saling bebas, digambarkan sebagai berikut :

                                                                     Gambar 4.7


P(B|A) = P(B∩A)/ P(A)

A = (B∩A) ∪ (B'∩A) : Saling asing/terpisah
⇒P(A) = P(B∩A) + P(B'∩A)

Jadi ⇒ P(B|A) = P(B∩A)/P(A) = P(B∩A)/P(B∩A)+P(B'∩A)

       ⇒ P(B|A) = P(B) P(A|B)/ P(B)P(A|B) + P(B') P(A|B')

Kaidah Peluang Total

Bila kejadian-kejadian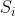  , i =1,2, ..., k adalah kejadian-kejadian tidak kosong dan saling asing, dengan 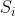  = S, maka untuk sembarang kejadian A himpunan bagian dari S berlaku :

            P(A) = P(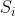 ) P (A| 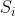) + P(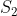) P(A|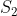) + ... + P() P(A|)

Teorema Bayes

Bila kejadian-kejadiana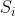   , i =1,2, ..., k adalah kejadian-kejadian tidak kosong dan saling asing, dengan 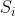   = S, maka untuk sembarang kejadian A himpunan bagian dari S dengan P(A)≠0 berlaku:

                                         P(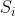|A) = P(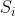) P(A|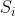)/ P(A)

dengan:
P(A) = P(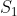 ) P(A| 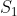) + P( 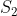) P(A|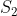) + ... + P() P(A|)

Contoh

1. Sebuah pabrik mempunyai 3 mesin A, B dan C yang memproduksi berturut-turut 60%, 30% dan 10% dari total banyak unit yang diproduksi pabrik.
Persentase kerusakan produk yang dihasilkan dari masing-masing mesin tersebut berturut-turut adalah 2%, 3% dan 4%.
Suatu unit dipilih secara random dan diketahui rusak.
Hitunglah :
Probabilitas bahwa unit tersebut berasal dari mesin C.

Jawab :
Dengan Teorema Bayes
Kejadian P(A), P(B) dan P(C) adalah (persentase produksi) dari masing-masing mesin
P(R | A), P(R | B) dan P(R | C) adalah peluang (persentase kerusakan) dari masing-masing mesin.

Jadi
⇒ P(C|R) = P(C) P(R|C) / P(A) P(R|A) + P(B) P(R|B) + P(C) P(R|C)

                 = (0,1) (0,04) / (0,6) (0,02) + (0,3) (0,03) + (0,1) (0,04)

                 = 0,16
2. Berikut adalah data peserta kuliah Metode Statistika di FSAINTEK UIN SUKA

    Tabel 4.2 Peserta kuliah Metode Statistika

                          Matematika            Biologi               Kimia                Jumlah
     Ganjil                     5                      10                       5                        20
     Genap                  20                       15                      35                       80
     Jumlah                 25                       35                      40                      100

Jika dipilih seorang siswa secara acak.
Tentukan:
a. Peluang terpilih mahasiswa ber-NIM ganjil
b. Peluang terpilih mahasiswa matematika. Jika diketahui mahasiswa tersebut ber-NIM ganjil

Jawab :

a. Peluang terpilih mahasiswa ber-NIM ganjil
    Menggunakan tabel diatas : P(Ganjil) = 20/100 = 0,2
    Kaidah peluang
    Didefinisikan terlebih dahulu
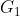     : Peristiwa terambil Mahasiswa bernomor Ganjil
    M   : Peristiwa terambil Mahasiswa Matematika
    F    : Peristiwa terambil Mahasiswa Fisika
    K   : Peristiwa terambil Mahasiswa Kimia

   P(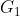 ) = P(M) P( 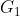|M) + P(F) P( 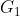|F) + P(K) P( 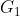|K)

               = 25/100 x 5/25 + 35/100 x 10/35 + 40/100 x 5/40

               = 0,2

b. Peluang terpilih mahasiswa matematika. Jika diketahui mahasiswa tersebut ber-NIM ganjil
    Menggunakan tabel diatas
    P (Matematika | Ganjil) = 5/20 = 0,25
    Teorema Bayes
    ⇒ P (M |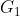  ) = P(M) P( 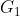|M) / P( )
               
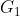                            = 25/100 x 5/25    = 0,25
                                        0,2

3. Ada 3 kotak yang masing-masing berisi 2 bola. Kotak I berisi 2 bola merah, kotak II berisi 1 bola merah dan 1 bola putih, dan kotak III berisi 2 bola putih.
Dengan mata tertutup anda diminta mengambil satu kotak secara acak dan kemudian mengambil bola 1 bola secara acak dari kotak yang terambil tersebut.
Anda diberitahu bahwa bola yang terambil ternyata berwarna merah. Berapakah peluangnya bola tersebut terambil dari kotak I, II dan III?

Jawab :
A1 = Kejadian terambilnya kotak I
A2 = Kejadian terambilnya kotak II
A3 = Kejadian terambilnya kotak III
B   = Kejadian terambilnya bola merah

Ditanya : P(A1/B), P(A2/B), dan P(A3/B)
Karena diambil secara acak maka :
P(A1) = P(A2) = P(A3) = 1/3

Probabilitas terambilnya bola merah dari kotak I :
P(B/A1) = 1

Probabilitas terambilnya bola merah dari kotak II :
P(B/A2) = 1/2

Probabilitas terambilnya bola merah dari kotak III :
P(B/A3) = 0

P(B) = P(B/A1). P(A1) + P(B/A2). P(A2) + P(B/A3). P(A3)
        = 1. 1/3 + 1/2 . 1/3 + 0.1/3
        = 1/2

Jadi :

P(A1|B) = P(B∩A1)/P(B) = P(B|A1) P(A1)/ P(B) = (1) (1/3)/ (1/2) = 2/3

P(A2|B) = P(B∩A2)/P(B) = P(B|A2) P(A2)/ P(B) = (1/2) (1/3)/ (1/2) = 1/3

P(A3|B)= P(B∩A3)/P(B) = P(B|A3) P(A3)/ P(B) = (0) (1/3)/(1/2) = 0