PELUANG BERSYARAT DAN INDEPENDENSI

Diketahui kejadian A dan B dengan P(B) > 0. Maka peluang bersyarat A jika B telah diketahui, P(A|B), didefinisikan sebagai :

P(A|B) =  P(A ⋂ B)/ P(B) ⇒ P(A|B) kejadian A dengan syarat B

atau

P(B|A) =  P(A ⋂ B)/ P(A) ⇒ P(B|A) kejadian B dengan syarat A

dari bentuk diatas akan diperoleh bahwa :


P(A ⋂ B) = P(A) P(B|A) atau P(A ⋂ B) = P(B) P(A|B)

secara umum dapat diperlihatkan bahwa :

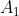P() = P(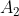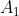) P(|) P(|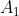∩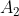)... P(|∩∩...∩)

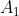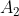Dua kejadian A dan B disebut kejadian saling independen jika

                                       P(A|B) = P(A) atau P(B|A) = P(B)

    Jika A dan B independen maka :
                       
                                     P(A ⋂ B) = P(A) P(B)

Secara umum, jika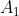  , 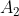, ...,  kejadian-kejadian saling independen, maka:

                           P(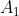) = P() P( 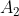) ... P( )

Contoh
1. Peluang suatu penerbangan yang teah terjadwal teratur berangkat tepat waktu adalah P(A) = 0,80;
    peluang B sampai tepat waktu adalah P(B) = 0,85; dan peluang suatu penerbangan berangkat dan
    sampai tepat waktu adalah P(A ⋂ B) = 0,75.
    Tentukan: Peluang pesawat berangkat tepat waktu jika diketahui sampai tepat waktu
    Jawab :

   ⇒P(A|B) =  P(A ⋂ B)/ P(B) = 0,75/0,85 = 0,88

2. Dua koin seimbang dilemparkan, dan diamati sisi yang terletak diposisi atas.
    Didefinisikan :
    A  : Sisi muka yang muncul pada koin I
    B  : Sisi belakang yang muncul pada II
    Selidiki, apakah peristiwa A dan B saling bebas?
    Jawab :

    S={MM,MB,BM,BB}
    A={MM,MB} → P(A) = 2/4 = 1/2 dan B = {MB,BM}
    A ⋂ B = {MB}→ P(A ⋂ B) = 1/4

    Dengan probabilitas bersyarat :
    Tampak P(A) = P(A|B). Jadi A dan B saling bebas