KAIDAH-KAIDAH PELUANG

Misalkan :
A = Suatu peristiwa /kejadian pada Ruang Sampel (S)
P(A) adalah peluang kejadian A, maka belaku :
1. 0 ≤ P(A) ≤ 1
2. P(S) = 1 (peluang dari ruang sampel) terjadi
3. P(⦲) = 0
    (peluang dari peristiwa yang tidak akan pernah terjadi)
4. Komplemen : Komplemen peristiwa A adalah Bukan A ditulis A' a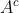tau  atau  .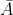
    Secara matematis :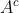    = {X ∈ S, x ∉ A}

                                        Gambar 4.2 Diagram venn Bukan A




   P(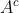 ) = P(A') = 1 - P(A)
   {Baca : Peluang kejadian bukan A}

Misalkan :
A dan B adalah 2 peristiwa/ kejadian pada Ruang Sampel (S)
P(A) dan P(B) adalah berturut-urut peluang kejadian A dan B, maka berlaku :

5. IRISAN dua kejadian A dan B, dinyatakan dengan A∩B, merupakan kejadian yang elemennya
    termasuk dalam A dan B.
    A ∩ B = { x ∈  S, x ∈ A dan x ∈ B}

 
                               Gambar 4.3 Diagram Venn A ∩ B


   Peluang irisan kejadian A dan B adalah ⇒ P(A ∩ B) = n(A ∩ B)/n(S)

6. GABUNGAN dua kejadian A dan B, dinyatakan dengan A ∪ B, merupakan kejadian yang
    mengandung semua elemen yang termasuk A atau B atau keduannya.
    A ∪ B = { x ∈  S, x ∈ A atau x ∈ B}

                               Gambar 4.4 Diagram Venn A ∪ B


   Peluang gabungan kejadian A atau B adalah ⇒ P(A ∪ B) = n(A ∪ B)/n(S)
   atau menggunakan aturan penjumlahan :
   P(A ∪ B) = P(A) + P(B) -  P(A ∩ B)

CONTOH
Pada pelemparan sebuah dadu dan mencatat angka dadu yang muncul
Ruang Sampel : S = {1,2,3,4,5,6}
Misalkan : A = Kejadian munculnya angka genap
                      = {2,4,6} maka n(A) = 3
                  B = Kejadian munculnya angka 5 atau lebih
                     = {5,6} maka n (B) = 2
Maka :
Komplemen dari A → A' = {1,3,5} maka n(A') = 3
Irisan A dan B → A ∩ B ={6} maka n (A ∩ B) = 1
Gabungan A dan B → A ∪ B = {2,4,5,6} maka n(A ∪ B) = 4

Sebagai Ilustrasi lihat gambar 4.5
Ruang Sampel

     Gambar 4.5



Jadi dapat dihitung :
a. Peluang kejadian A
   ⇒ P(A) = n(A)/n(S) = 3/6 = 1/2

b. Peluang kejadian bukan A
  ⇒ P(A') = 1 - P(A) = 1 - 1/2 = 1/2

c. Peluang kejadian A dan B
  ⇒ P(A ∩ B) = n(A ∩ B)/ n(S) = 1/6

d. Peluang kejadian A atau B
  ⇒P(A ∪ B) = n(A ∪ B)/ n(S) = 4/6 = 2/3

7. Dua kejadian A dan B dikatakan saling terpisah asing (mutually exclusive) jika kejadian-
    kejadian tersebut tidak dapat terjadi secara bersamaan
    ditulis : (A ∩ B) = ⦲

                                 Gambar 4.6 Diagram venn dua kejadian saling asing


  Akibatnya :
  IRISAN                      : P(A ∩ B) = 0
  GABUNGAN            : P(A ∪ B) = P(A) + P(B)

CONTOH

1. Pada pelemparan sebuah dadu. Misalkan:
    A  = Kejadian munculnya angka genap = {2,4,6}
    B  = Kejadian munculnya angka ganjil = {1,3,5}
    A dan B adalah 2 kejadian yang terpisah / saling asing

2. Pada setumpuk kartu Bridge diambil sebuah kartu secara acak. Didefinisikan peristiwa-
    peristiwa:
    A = Kartu terambil adalah hati
    B = Kartu terambil adalah As
    C = Kartu terambil berwarna hitam
    A dan B : tidak terpisah / saling asing
    A dan C : terpisah/ saling asing
    B dan C : tidak terpisah/ saling asing

  8. Dua kejadian A dan B : saling bebas (independen) jika berlaku: P(A ∩ B) = P(A)P(B)
CONTOH
Pada pelemparan sebuah dadu. Misalkan :
A = Kejadian munculnya angka genap pada lemparan 1
B = Kejadian munculnya angka ganjil pada lemparan ke-2 A dan B adalah 2 kejadian yang saling bebas

Jadi
Dapat dihitung peluang muncul angka dadu genap pada pelemparan 1 dan ganjil pada pelemparan ke 2 :

⇒ P(A ∩ B) = P(A)P(B) = 1/2 x 1/2 = 1/4